【Grasshopper_28】Crystallonを使ってウサギをラティス形状に加工してみた

前回に引き続き､Lattice構造作成プラグインであるCrystallonを使った事例を紹介します。

<事前準備>

次のプラグインをダウンロードして所定のフォルダに格納する。
・Crystallon V2
・Lunch Box
・Weaver bird
・Topologizer
・MeshMachine.gha
・Plankton.gha
・Plankton.dll

Step1.データを用意する

まずはポリゴンデータを準備します。
今回使用したのはStanford Bunnyと呼ばれる､CG環境のベンチマーク等に使われる、有名なポリゴンデータです。ググるとダウンロードリンクが出てきますので、各自で用意します。

Step2.メッシュデータをインポートする

・まず､Stanford BunnyをRhinoにインポートし、スケールを2倍に拡大します。これでほどよい大きさになります。

Step3.ポリゴン数を減らす

・メッシュの密度が細かいと計算に時間がかかるので、もう少し密度を粗くします。

・Lunch Boxプラグインの中にある､Mesh ReduceコンポーネントにウサギのMeshをつなぎ、メッシュ数を減らします。今回は1500個にしています｡

Step4.ポリゴンを再構成する

・上の図はStep.3でメッシュの数を減らした状態ですが､三角メッシュの形がバラバラで､なるべく正三角形に近い方がLatticeの形が綺麗になります。そこで、リメッシュと呼ばれる、メッシュの再構築作業に進みます。

こちらの記事を参考にしました↓

Step5.ポリゴンを再構成する　その2

・上記ブログの真ん中から下寄りに各種ダウンロードリンクがありますので、MeshMachine.gha、Plankton.gha、Plankton.dllはダウンロードして所定のフォルダに格納します(Rhinoの再起動が必要です)。

・一番下のRemesh_new_examples.ghがいくつかのサンプル集となっていて、この中から選びます。今回は､このように組みました↓

・左上のMesh端子に、Step.3で出力したメッシュデータをつなぎます。
・メッシュの大きさを決めるのがLengthの数値ですが、なるべく大きくしたいところですが大きすぎるとエラーになりますので、ぎりぎりの数値を調整しながら決めます。

・上の図のTimerコンポーネントのEnabledをONにすると自動的に解析がスタートします。延々と続くので、適当なところでTimerコンポーネント(5msと書いてあるアイコン)を右クリックし、Enabledをoffにしてタイマーを停止させて確認します｡

多少、形は壊れてますが、それなりに綺麗に三角形メッシュができました。

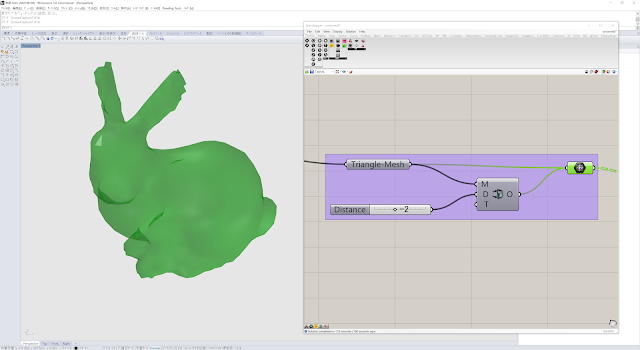
Step7.メッシュをオフセットさせる

・Step.6で求めたメッシュデータをWeaver birdのOffset Meshコンポーネントを使って内側にオフセット処理を行います｡ここではとりあえず、-2mmにしています。

Step8.Voxelを作成する

・CrystallonのMorph Between Meshesコンポーネントを使い、2つのMesh間にVoxelを作ります。

・Tri入力はTrueにします。これは、三角形ポリゴンの場合にTrue、四角形ポリゴンの時にFalseにしておく部分です｡Trueにすると、三角形が自動的に辺の中心で分割され、1つの三角形ポリゴンが4つの四角形ポリゴンに分割されます｡内部計算的には四角形ポリゴン専用なのかもしれません。

・CrystallonのCell Selector、Cell Lattice Fill、Cell Typeコンポーネントを上図のようにつなげてLattice構造を配置します。

・今回は、Prim.Cubicという、最もベーシックな構造にしました。

Step10.カーブを中心にPipeサーフェスを作成する

・Step.9で求めたLattice構造体はLine-like Curveとなっているため､End PointsコンポーネントとLineコンポーネントを使ってLineに置き換えます｡

・その後､Topologizerコンポーネントを使って2重に重なるカーブを除去した後､Pipeコンポーネントで3D化します。

※今回はCG用で作るため簡易的にPipe形状にしましたが、3Dプリンターで出力する場合はメッシュ化することをお勧めします。

Step11.CG化

以前の記事で紹介した、Neonによるレンダリングをしました。