【Grasshopper_90】Kangaroo2のOrigami foldingを試してみました

今回はOrigami Foldingについてチャレンジしてみました。

Origami Foldingとは、紙を折るような動作を物理演算機能を使って再現したものですが、Origami Foldingという機能そのものがあるのではなく、Kangaroo2に含まれている、いくつかのコンポーネントを組み合わせて再現するということがわかってきました。

物理演算というと、一般的にはエンジニア向けの機能という認識であり、カーデザイン分野では使用する機会が無いと思いがちですが、今回の話題であるOrigami Foldingについてはインテリア、エクステリア問わず面白い表現ができるのではないかと感じます。

そこで、今回はOrigami Foldingに特化した、簡単な使い方を順を追って紹介していきます。

物理演算機能「Kangaroo2」とは

・物理演算というとフックの法則だとか重力、加速度などのように、高校の物理の授業で習う知識が必要かと思われがちですが、Kangaroo2ではあまりそれらの知識がなくても感覚的に使えるように配慮されています。

・仕組みをものすごく簡単に言えば、ポリゴンメッシュの頂点に力を加えたり、位置を固定したりすることで、その設定した条件下でポリゴン面を変形させる機能です。

「頂点に力を加える、位置を固定する」とは現実世界での物理現象を指しますが、CAD上では点を指定した方向と距離で移動させるということを指します。そして、その方向や移動量を様々な条件の元で計算する部分をKangaroo2という名称のコンポーネントが担っています。

1. ひし形1個の折り方

まずは基本からということで、ひし形1個だけの状態で折ってみます。

・XY平面上に、少々縦長のひし形を一つ、作成します。

・中心から各頂点までの直線(緑色)を4本、中心からエッジ中点までの直線(赤色)を4本作成し、ひし形サーフェスを全直線を使って8つの三角形サーフェスに分割します。

・次が、Kangaroo2本体の部分です。こちらについては細かく解説していきます。

・Solverコンポーネントです。演算機能の本体ですね。PCで言うならばCPUみたいな存在です。各種条件はすべてGoalObjectsにつなぎ、Flattenにしておきます。

・Resetの入力はButtonをつなぎます。変形を初期の状態に戻すたびにこれを押します。

・OnはいわゆるON/OFFスイッチです。計算がOnの状態だとCPUに負荷がかかるので、使わない時はToggleをFalseにしておきます。

・計算結果はO出口から取り出します。

・電球の絵が書かれているコンポーネントがShowコンポーネントです。Solverコンポーネントから取り出せるデータは通常、カーブのみですが、変形後のポリゴンメッシュも出力したいときは、ポリゴンメッシュをShowコンポーネントを経由させてSolverのGoalObjectsにつなぎます。

・Kangaroo2で変形させるデータはポリゴンメッシュになりますので、8つに分割したサーフェスは、Simple Meshコンポーネントにつないでポリゴンメッシュに変換した後、Weaverbird's Join Meshes and Weldにつないで一つのメッシュに結合します。ウェルド作業を行うと折れる形があまり綺麗ではないので、WはFalseのままにしておきます。

・Lengthコンポーネント。ポリゴンを変形させる際、ポリゴンのエッジの長さをどの程度まで延長もしくは収縮させるかを決めるところです。Lengthのところに、延長もしくは収縮させたい場合は具体的な数値を入力できますし、変形後も同じ長さにしておきたいときはエッジそのものをつないでもOKです(今回は後者の方です)。

・Strengthについては、強度的な意味合いを持つのかと思われますが、他のシミュレーションソフトとは異なり、何か具体的な物理量を持っているわけではなく、あくまでも他の条件に関連するコンポーネントに対しての優先度的な数値になるようです。ほかの条件よりも少し程度を強めたいなと感じた時に適当な数値をつなぐようですが、デフォルトで10が設定されておりますので今回はそのままで大丈夫です。

・Floorコンポーネント。床面(ここではXY平面)に押し付けるような力をかける機能です。これは無くてもいいぐらいですが、緩やかにXY平面方向に力をかけておくために0.1という数字をつないでいます。

・Hingeコンポーネント。これがいわゆる「折る」設定です。

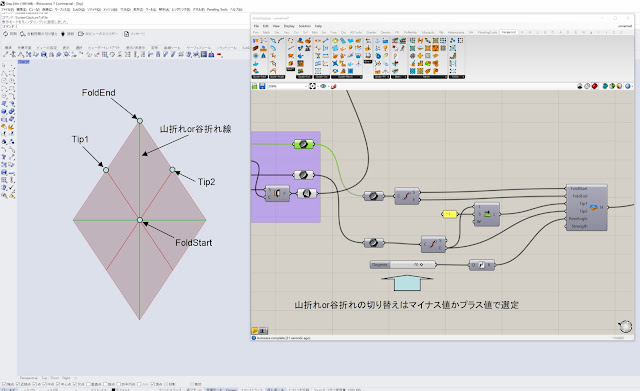
・はじめに、実際に折る場所を線で決める必要があります。今回のケースでは上の図の緑色の線となりますので、緑色の直線の始点と終点をそれぞれFoldStart、FoldEndにつなぎます。FoldStart側が基点となりますので、凹凸の変化が大きい方がFoldStartという感じです。

・冒頭で説明した通り、Kangarooはポリゴンの頂点に力を加えてポリゴンメッシュを変形させる機能です。今回のケースでは、緑色の折れ線に対し、両隣にある頂点に力を加えて折ることになりますので、Tip1とTip2は赤色の直線の終点に相当することがわかります。Tip1とTip2は緑色の折れ線を境にそれぞれ反対側にある必要がありますので、Shift Listコンポーネントを使ってリスト内の順番を一つずらすことで、どちらかをTip1、Shift ListでずらしたほうをTip2とすることができます。

・実際に折る角度はRestAngleにつなぎます。単位がRadianですので単位変換します。山折れと谷折れの切り替えは、マイナス値かプラス値で決まりますのでスライダーで調整します。

※ポリゴン面自体はすべてつながっているため、赤色の直線部分も結果的には折れることになりますが、少し緩やかな折れ方になります。

・出力結果はMeshとLineですので、Match Textコンポーネントを使って、それぞれ分類して表示してみました。

2. 複数の正方形の折り方

・次は、正方形を縦横に並べて折ってみます。基本的な考え方は同じですね。

・Lunch BoxプラグインのQuad Panelsコンポーネントを使って正方形を敷き詰めてから、中心と頂点までの直線4本とエッジ中点までの直線4本を各セルごとに求めます。

・折れ線は、上の図の緑色の線です。斜め方向につながるような感じです。

・物理演算の部分です。先ほどの1.とほぼ同じですが、拘束条件を追加しています。

・ポリゴンメッシュの全頂点をDeconstruct Meshコンポーネントにつないで求め、ダブり点を削除した後にAnchorXYZコンポーネントを使ってZ方向のみ移動できるよう方向を規制します。方向を規制しない場合、下の図のようにグニャッと曲がるような形になってしまいます。ただし、本来の折り紙という感じにはなりますね。

・最後にデータを取り出したら完成です。

3. 折り目の位置を変更したひし形の折り方

・次は、ひし形の折り方ですが、折り目の位置を少し変えてみたものです。

・Lunch BoxプラグインのDiamond Panelsコンポーネントを使ってひし形を敷き詰めます。

・ひし形を行ごとに互い違いに分類する必要があるため、上の図のようなノードを構築し、2種類のサーフェスを取り出します。詳細の説明は省きます。

・折れ線を作る部分です。今回の折れ線は、上の図の緑色の線になります。

・先ほど分類したサーフェスの、エッジ上の点をそれぞれEvaluate Curveコンポーネントにつなぎ、上の図のような直線の位置になるように0から1の間の数値を調整します。片方のエッジ上の点(t値)が0.1だとしたら、もう片方のエッジ上の点(t値)は1 - 0.1 = 0.9という考え方です。

・最後にPath Mapperコンポーネントを使い、Mergeした後のパス階層がきれいにつながるように変更してからそれぞれ一つにまとめます。

・物理演算の部分は先ほどの2.と同じです。

4. 大きさを徐変させたひし形の折り方

・次は、ひし形の大きさを変化させた状態で折ってみます。

・適当な正方形の形をしたレクタングルを作成し、Graph Mapperコンポーネントにつないで間隔を変化させたisoカーブを求め、U方向もしくはV方向の線を使ってControl Point Loftコンポーネントにつなぎサーフェスをそれぞれ作成します。

・作成した一方のサーフェス上に、Diamond Panelsコンポーネントにつないでひし形を作成し、もう一方のサーフェスにマッピングし、最後にBoundary Surfacesコンポーネントにつないでサーフェス化します。

・さきほどの3.と同じく、行ごとにサーフェスを分類します。

・折れ線を求める部分。こちらもさきほどの3.と同じ手順です。

・物理演算の部分も3.と同じです。

5. 折る角度を徐変させてみる

・最後に、ひし形の折り方の応用編ということで、折る角度を中心に向かって徐々に大きくしつつ、外周のエッジ部分は頂点の位置を完全拘束する方法を考えてみます。

・ひし形を作って行ごとに分類します。先ほどの4.と同じです。

・折れ線を作ります。これも先ほどの4.と同じです。

・次に物理演算の部分ですが、拘束条件とヒンジ設定の個所で少々改良を加えました。

・拘束条件については、今回は最も外側の頂点(上の図の赤色の頂点)が完全拘束、それより内側の頂点(上の図の緑色の頂点)はX、Y方向のみ拘束という2種類の条件を作りたいところですが、Kangaloo2のSolverにはAnchorコンポーネントは一つしかつなげることができません。そこで回避手段として、以下のような方法を考えてみました。

はじめに全頂点をAnchorXYZコンポーネントにつなぎ、すべてTrueにして完全拘束する。

→次に、全サーフェスをBrep Join、Brep Edges、Join Curvesコンポーネントにつないで外周エッジを求めた後、1mmほど内側にオフセットさせ、その曲線の内側にある点及びそのインデックス番号を抽出する。

→次に、抽出した点をもう一つのAnchorXYZコンポーネントにつなぎ、Z方向のみFalseにセットする。

→最後に、Replace Itemsコンポーネントにつなぎ、抽出したインデックス番号に該当する箇所のみ入れ替える。

・Hingeコンポーネントの角度の徐変量計算の部分です。

・徐変量の計算は、Nudibranchプラグインを利用します。Curve ValuesコンポーネントのC入力は計算の基準となるカーブをつなぎますので、さきほどの拘束条件の設定のところで求めた外周エッジ部の閉曲線をつなぎ、P入力はFoldStartの点をつなぎます。

・Curve ValuesコンポーネントのP入力は計算の都合上、Flattenにより平坦化する必要がありパスの階層がフラットになってしまうので、Remap Numbersコンポーネントの後ろでUnflatten Treeコンポーネントにつないでパスの階層構造を元に戻しています。

・以上で完成です。

折り目の位置を変更したりすることで色々な形に変化するので、オリジナルな形を作ってみるのも面白いですね。

今回は単純な正方形とかひし形の折り方を紹介しましたが、より複雑な、これぞGrasshopper的な折り方を現在研究中ですので、次回の記事で紹介できればと考え中。