【Grasshopper_32】2本のカーブを使った大きさのグラデーション方法

コロナの影響でしばらく在宅勤務となってしまったので、勉強も兼ねて、空いた時間を使ってこんな感じのものを作って見ました。

Step1.XY平面上に六角形を敷き詰める

・まずはLunchBoxのHexagonCellsコンポーネントを使い、適当な範囲に六角形を配置します。

・六角形じゃなくても、何でもOKです｡

Step2.オフセットさせる

・敷き詰めた六角形をオフセットさせます。距離は適当です。

Step3.外周部分を削除する

・Step.1で敷き詰めたパターンのうち、外周部分にある六角形の片割れ部分は必要がないので、削除します。

・Explodeコンポーネントで辺を分解した後、数が6個かどうかEqualityコンポーネントで判別させた上で、Cull Patternコンポーネントを通して仕分けします｡

・特に外す必要がなければこの工程はスルーしてもOKです。

Step4.2本のカーブを作成する

・ライノ上で適当な曲率の自由曲線を2本作成し､Grasshopperに取り込みます。

Step5.パターンを分類する

・取り込んだ2本のカーブを使って、六角形のパターンを3個所に分類します｡

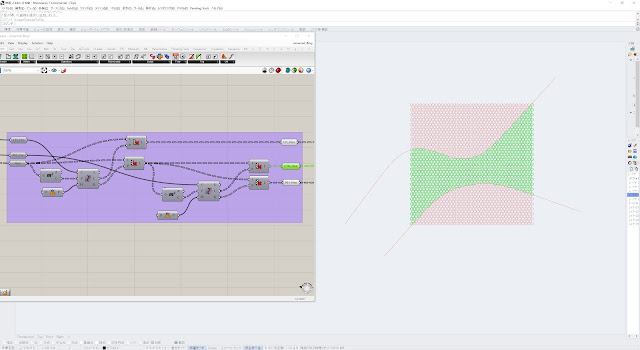
・六角形の中心点をAreaコンポーネントを使って求め、その中心点がそれぞれのカーブの外側か内側かをCurve Sideコンポーネントで判別させ､Cull Patternコンポーネントを使って分類します。

Step6.パターンを縮小させる

・2本のカーブの間のパターンをスケールダウンさせます。

・考え方としては、六角形の中心点を求め、2本のカーブまでの最短距離をそれぞれ求めます｡

・求めた2つの最短距離の大きさを比較し、小さい方の数値をMinimumコンポーネントを使って選択します。

・求めた距離を、Remapコンポーネントを使い､実際のスケール値のレンジに変換します｡2本のカーブに近いほうがよりスケールが大きいので、Construct DomainのAが1に近く、Bが0に近くなるようにします。

・2本のカーブの中央付近は最小の大きさを一定の割合で増やすため、Larger Thanコンポーネントを使い､0.05より小さな値はすべて0.05に置き換えています。

Step7.完成

・最後に、すべての六角形をまとめると完成です。