【Grasshopper_55】Grasshopperプラグイン「PanelingTools for Rhino and Grasshopper」の簡単な使い方の紹介

Paneling Toolsというプラグインを使って簡単なサンプルを作ってみたので今回はその紹介です｡

このプラグインはかなり以前から存在するもので、その存在自体は知っていましたが､特に不自由なくモデリングが出来ていたため､これまでほとんど触ったことがなかったのですが､実際に使ってみるとなかなか便利だなと感じました｡

基本的には2Dもしくは3Dのサーフェス上に点群(グリッド)を作成し、その点群を使って長方形やひし形、六角形などの幾何学形状を作るのが主な使用目的です。

今まではLunch Boxで幾何学パターンを作り､Nudibranch、あるいは自作のコンポーネントで大きさの変化をつけるという工程でしたが、PanelingToolsは単体で完成しますので、ノード構成も短くてすみそうです。

このプラグインの機能はかなり多岐に渡ります｡詳細な機能が知りたい場合は､以下のリンク先にあるドキュメントを参照ください｡

ダウンロードは以下のリンクからどうぞ。

2Dパターン作成編

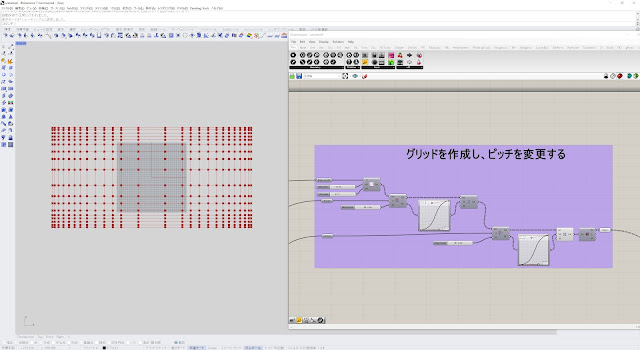
Step.1 XY平面上に長方形を作成する

・適当な大きさの四角形をXY平面上に作成します｡

・同時に､MDスライダーで指定する場所にisoカーブを作成します｡

　今回のサンプルでは、カーブを基準に各点までの距離を測定し、四角形の大きさ変化に使用します(いわゆる、Curve Attractorという機能です)｡

Step.2 四角形の大きさを変化させる

・次に、いきなりpaneling toolsのコンポーネントを6つ繋ぎます｡これだけで､四角形を作り､さらに大きさの変化までできます｡

・左から順に､

　①Surface Domain Number : 

　　サーフェスを指定の数値で分割し､その点群を求めます｡この時点では均等な大きさに分割した状態での点群が生成されます。

左右対称形状にしたい場合、横方向の数を奇数にします。

　

　②Curve Attraction : 

　　カーブを測定基準とし、①で求めた点群を距離に応じて移動させます。ここでは縦方向に変化させています。スライダーで調整可。

　③Weight Attaraction : 

　いわゆる重み付けによる変化です。②のCurve Attractionのみだと、変化の仕方が直線的で徐々に変化する感じが皆無なので、重みによる変化をつけます。②のCurve AttractionコンポーネントのW出力から取り出せる0～1の範囲の数値をGraph Mapperで変化させ、Weight Attractionコンポーネントにつないでいます｡

 ④Curve Attraction : 

　次は同じく、Curve Attractionコンポーネントをつなぎます。ここでは横方向に変化させます。

　⑤Weight Attaraction : 

　③と同じく重み付けによる変化です。

　⑥Cellurate : 

　点群の位置は①～⑤で決まったので、四角形に変換します。このコンポーネントをつなぐだけで、自動的に閉じた曲線が生成されます。

Step.3 徐変四角形の完成

・後はお好みで仕上げて完成です。

・isoカーブの位置をMDスライダーでいじったり、徐変の割合をGraph Mapperでいじったりすると自在に変形が可能です。

次に、ひし形の作成手順に移ります。

Step.4 長方形を作成する。

・この工程は、Step.1と全く同じなので、コピペでOKです｡

Step.5 ひし形の作成

・この工程はStep.2とほぼ同じですが､唯一異なるのは二つ目のWeight AttractionとCellurateの間にConvert to Diamondコンポーネントを挟んでいます。これで、ひし形ができます。

Step.6 徐変ひし形の完成

・後はお好みでいじって完成です。

次に、六角形の作成に移ります。

Step.7 XY平面上に四角形を作成する

・Step.1と同じです｡ここでは､参照点までの距離に応じた大きさの変化をつけますので(いわゆるPoint Attractionです)､isoカーブではなく、Construct Pointコンポーネントを使って点のUV座標を決めます。

Step.8 六角形の作成

・基本的な考え方はStep.2と同じです。まずは、Surface Domain Numberコンポーネントにつないで分割数に応じた点群を作成します。

・Step.７で指定した､点のUV座標値にしたがって、Evaluate Surfaceコンポーネントを通して点の座標値を求め､Point Attractionコンポーネントにつないで距離に応じた位置まで点を移動させます。

・Graph MapperとWeight Attractionにつないで重み付けによる点群の位置調整を行います｡

・その次に､Panel Connectionsコンポーネントにつなぎます。六角形そのものを作るコンポーネントが現時点ではこのプラグインに用意されていないため、公式掲示板に記載の情報に従って、黄色のPanelに記載された点のインデックスをそのままつないで、2種類の多角形を作成します｡

・出来上がる多角形は端末付近の三角形の部分も含みますので､Explodeコンポーネントを使って辺を分解し、3本のみの階層をCullパターンコンポーネントを通して除去し､六角形のみ取り出します｡

Step.9 徐変六角形の完成

・後はお好みで加工したら完成です。

3Dパターン作成編

次に､3Dサーフェス上に直接、パターンを作る方法に移ります。

Step.10 適当な3Dサーフェスを用意する

・各自､お好みでサーフェスを用意します｡Rhinoで作ったものでもOKです。今回は上の図のような、Grasshopperで作ったサーフェスを用意します。一番右にあるコンポーネントはLunch Boxに含まれる､Rrebuild Surfaceです。

Step.11 3Dサーフェスを縮小させ、isoカーブを求める

・今回のケースではくり抜き形状を作るので、IsoTrimコンポーネントを使って､若干､サーフェスを縮小させ、パターンを配置させるエリアとしまｓ｡

・パターンの大きさの変化の基準として､Step.1と同じくUとVのカーブを求めます｡

Step.12 四角形を3Dサーフェス上に作成する

・基本的な考え方はStep.2と同じです。異なるのは、Pull Point及びPull Curveコンポーネントを使って、点群及びカーブを3Dサーフェス上に面直投影している個所です。これを挟まないと、四角形が壊れてしまいます。

Step.13 徐変四角形(3D)の完成

・後はお好みで加工したら完成です｡

次にひし形の作成に移ります｡

Step.14 3Dサーフェスを縮小させ、isoカーブを求める

・Step.11と同じです｡位置が重ならないよう､Y方向に移動させています。

Step.15 四角形を3Dサーフェス上に作成する

・Step.12とほぼ同じです。2D版と同じく､Convert to Diamondコンポーネントを挟んでいます。

Step.16 徐変ひし形(3D)の完成

・後はお好みで加工したら完成です｡

次に六角形の作成に移ります｡

Step.17 3Dサーフェスを縮小させ、isoカーブを求める

・Step.11とほぼ同じです。ここでは、Point Attractionを使いますので､参照点のUV座標値を決めています。

Step.18 六角形を3Dサーフェス上に作成する

・Step.8の3D版です｡

Step.19 徐変六角形(3D)の完成

・後はお好みで加工したら完成です｡